圖可以定義為用於連接這些頂點的頂點和邊的組。 圖可以看作是迴圈樹,圖中頂點(節點)維持它們之間的任何複雜關係,而不是簡單的父子關係。
1. 圖定義
圖G 可以定義為有序集G(V,E),其中V(G)表示頂點集,E(G)表示用於連接這些頂點的邊集。
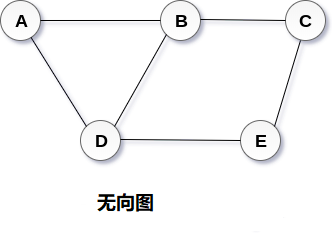
圖G(V,E)有5個頂點(A,B,C,D,E)和6個邊((A,B),(B,C),(C,E),(E,D), (D,B),(D,A))如下圖所示。
2. 有向圖和無向圖
圖可以是有向的或無向的。 但是,在無向圖中,邊與它們的方向無關。 上圖中顯示了無向圖,因為其邊未與任何方向相連。 如果在頂點A和B之間存在邊,則頂點可以從B遍曆到A以及從A到B遍曆。
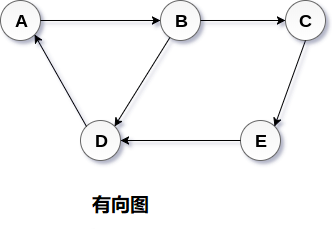
在有向圖中,邊形成有序對。 邊表示從某個頂點A到另一個頂點B的特定路徑。節點A稱為初始節點,而節點B稱為終端節點。
有向圖如下圖所示。
3. 圖技術
3.1. 路徑
可以將路徑定義為遵循的節點序列,以便從初始節點U到達某個終端節點V。
3.2. 閉合路徑
如果初始節點與終端節點相同,則將路徑稱為閉合路徑。 如果V0 = VN,則路徑將是閉合路徑。
3.3. 簡單路徑
如果圖的所有節點都是異常的並且異常V0 = VN,那麼這種路徑P被稱為閉合簡單路徑。
3.4. 週期
週期可以定義為除了第一個和最後一個頂點之外沒有重複邊或頂點的路徑。
3.5. 連通圖
連通圖是在V中的每兩個頂點(u,v)之間存在一些路徑的圖。連通圖中沒有孤立的節點。
3.6. 完整圖
完整圖是每個節點與所有其他節點連接的圖。 完整圖包含n(n-1/2個邊,其中n是圖中節點的數量。
3.6. 權重圖
在權重圖中,為每個邊分配一些數據,例如長度或重量。 邊e的權重可以給定為w(e),其必須是指示穿過邊緣的成本的正(+)值。
3.7. 有向圖
有向圖是有向圖,其中圖的每個邊與某個方向相關聯,並且只能在指定的方向上進行遍曆。
3.8. 迴圈
與類似端點相關聯的邊可以稱為迴圈。
3.9. 相鄰節點
如果兩個節點u和v通過邊e連接,則節點u和v被稱為鄰居或相鄰節點。
3.10. 節點的度
節點的度數是與該節點連接的邊的數量。 度為0的節點稱為隔離節點。
