廣度優先搜索(BFS)演算法

在本教學的這一部分中，將討論使用哪些技術，可以遍曆圖的所有頂點。
遍曆圖表表示訪問圖的所有節點和頂點。 使用兩種標準方法，可以遍曆圖。接下來將詳細討論它們中。

• 廣度優先搜索
• 深度優先搜索

1. 廣度優先搜索(BFS)演算法

廣度優先搜索是一種圖遍曆演算法，它從根節點開始遍曆圖並探索所有相鄰節點。 然後，它選擇最近的節點並流覽所有未探測的節點。 對於每個最近的節點，該演算法遵循相同的過程，直到找到目標為止。

下麵給出了廣度優先搜索的演算法。演算法從檢查節點A及其所有鄰居開始。在下一步中，搜索A的最近節點的鄰居，並且在後續步驟中繼續處理。 該演算法探索所有節點的所有鄰居，並確保每個節點只訪問一次，並且沒有訪問任何節點兩次。

演算法

第1步：設置狀態 = 1(就緒狀態)
    對於G中的每個節點

第2步：將起始節點A排隊
    並設置其狀態 = 2
    (等待狀態)
第3步：重複第4步和第5步，直到
    佇列是空的

第4步：使節點N出列。處理它
    並設置其狀態 = 3
    (處理狀態)。

第5步：將所有鄰居排隊

      N處於就緒狀態

 (其STATUS = 1)並設置它們狀態 = 2
 (等待狀態)
  [迴圈結束]
第6步：退出

示例

考慮下圖中顯示的圖G，計算從節點A到節點E的最小路徑p。給定每條邊的長度為1。

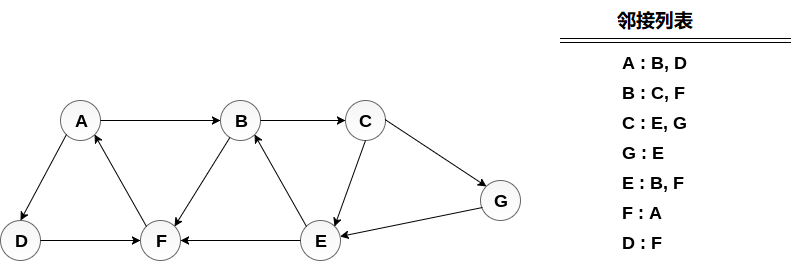
解答：

最小路徑P可以通過應用廣度優先搜索演算法找到，該演算法將從節點A開始並將以E結束。演算法使用兩個佇列，即QUEUE1和QUEUE2。 QUEUE1保存要處理的所有節點，而QUEUE2保存從QUEUE1處理和刪除的所有節點。

下麵來看看節點A 中的圖。

1. 將A添加到QUEUE1，將NULL添加到QUEUE2。

   QUEUE1 = {A}
   QUEUE2 = {NULL}
   

2. 從QUEUE1中刪除節點A並插入其所有鄰居，將節點A插入QUEUE2。

   QUEUE1 = {B, D}
   QUEUE2 = {A}
   

3. 從QUEUE1中刪除節點B並插入其所有鄰居。 將節點B插入QUEUE2。

   QUEUE1 = {D, C, F}
   QUEUE2 = {A, B}
   

4. 從QUEUE1中刪除節點D並插入其所有鄰居。 由於F是已插入的唯一鄰居，因此不會再插入它。 將節點D插入QUEUE2。

QUEUE1 = {C, F}
QUEUE2 = { A, B, D}

1. 從QUEUE1中刪除節點C並插入其所有鄰居。 將節點C添加到QUEUE2。

   QUEUE1 = {F, E, G}
   QUEUE2 = {A, B, D, C}
   

2. 從QUEUE1中刪除F並添加其所有鄰居。由於已經添加了所有鄰居，不會再添加它們。 將節點F添加到QUEUE2。

QUEUE1 = {E, G}
QUEUE2 = {A, B, D, C, F}

1. 從QUEUE1中刪除E，所有E的鄰居都已添加到QUEUE1，因此不會再添加它們。 訪問所有節點，並且目標節點即E遇到QUEUE2。

QUEUE1 = {G}
QUEUE2 = {A, B, D, C, F,  E}

現在，使用QUEUE2中可用的節點從E回溯到A。

最小路徑為：A→B→C→E。