B樹是一種專用的M階樹,可廣泛用於磁片訪問。 M階樹順序的B樹最多可以有m-1個鍵和M個子樹。 使用B樹的主要原因之一是它能夠在單個節點中存儲大量鍵,並且通過保持樹的高度相對較小來存儲大鍵值。
排序M的B樹包含M階樹的所有屬性。 此外,它還包含以下屬性。
- B樹中的每個節點最多包含
m個子節點。 - 除根節點和葉節點外,B樹中的每個節點至少包含
m/2個子節點。 - 根節點必須至少有
2個節點。 - 所有葉節點必須處於同一級別。
所有節點都不必包含相同數量的子節點,但每個節點必須具有m/2個節點數。
在下圖中顯示了4階B樹。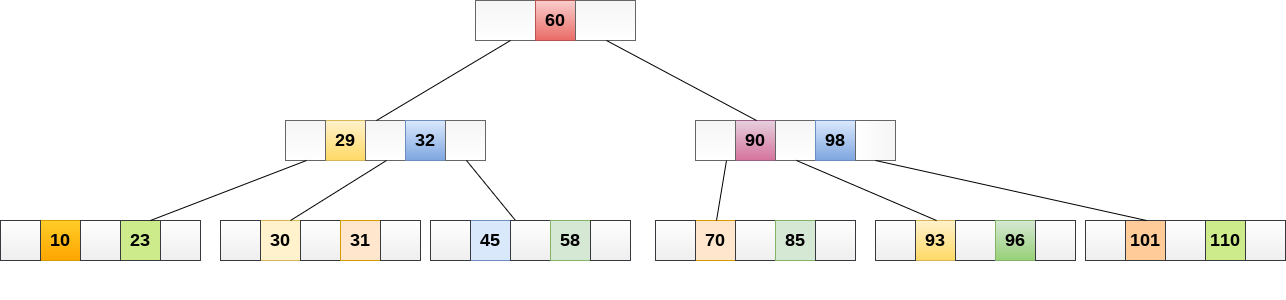
在B樹上執行某些操作時,B樹的任何屬性都可能違反節點可以擁有的最小子節點數。 為了維護B 樹的屬性,樹可能會分裂或連接。
操作
1. 搜索
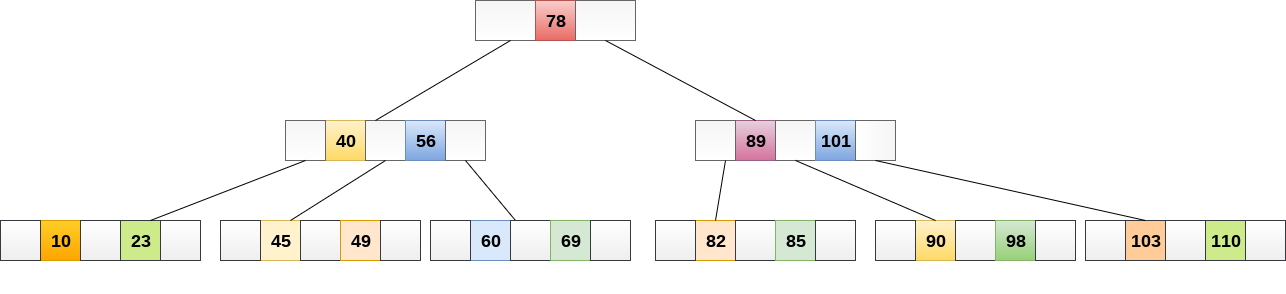
在B樹中搜索類似於二叉搜索樹中的搜索。 例如,如果在以下B樹中搜索資料項目:49。 該過程將如下所示:
- 將資料項目
49與根節點78進行比較。因為49 <78因此,移動到其左子樹。 - 因為,
40 <49 <56,遍曆右子樹40。 49> 45,向右移動。 比較49。- 找到匹配,則返回。
在B樹中搜索取決於樹的高度。 搜索演算法需要O(log n)時間來搜索B樹中的任何元素。
2. 插入
插入在葉節點級別完成。要將專案插入B樹,需要遵循以下演算法。
- 遍曆B樹以找到可插入節點的適當葉節點。
- 如果葉節點包含少於
m-1個鍵,則按遞增順序插入元素。 - 否則,如果葉節點包含
m-1個鍵,則按照以下步驟操作。- 按元素的遞增順序插入新元素。
- 將節點拆分為中間的兩個節點。
- 將中值元素推送到其父節點。
- 如果父節點還包含
m-1個鍵,則按照相同的步驟將其拆分。
示例:
將節點8插入到下圖所示的5階B樹中。

8將插入5的右側,因此插入8。

該節點現在包含5個鍵,大於(5 -1 = 4)個鍵。 因此,將節點從中間分開,即8,並將其推到其父節點,如下所示。

3. 刪除
還在葉節點處執行刪除。 要刪除的節點可以是葉節點或內部節點。 需要遵循以下演算法才能從B樹中刪除節點。
- 找到葉節點。
- 如果葉節點中有多於
m/2個鍵,則從節點中刪除所需的鍵。 如果葉節點不包含
m/2個鍵,則通過從8個或左兄弟中獲取元素來完成鍵。- 如果左側兄弟包含多於
m/2個元素,則將其最大元素推送到其父元素,並將插入元素向下移動到刪除鍵的節點。 - 如果右側兄弟包含多於
m/2個元素,則將其最小元素向上推送到父節點,並將插入元素向下移動到刪除鍵的節點。
- 如果左側兄弟包含多於
如果兄弟節點都不包含多於
m/2個元素,則通過連接兩個葉節點和父節點的插入元素來創建新的葉節點。- 如果父節點的節點少於
m/2,那麼也應在父節點上應用上述過程。 - 如果要刪除的節點是內部節點,則將節點替換為其有序後繼或前一個節點。 由於後繼或前任將始終位於葉節點上,因此該過程將類似於從葉節點中刪除節點。
示例1
從下圖所示的5階B樹中刪除節點:53。
元素49的右子節點中存在53,則刪除它。
現在,57是唯一留在節點中的元素,在5階B樹中必須存在的最小元素數是2。它小於左邊和右邊子樹中的元素 因此,也不足以將其與父母的左兄弟和干預元素合併,即49。
最終的B樹如下所示。

B樹的應用
B樹用於索引數據並提供對存儲在磁片上的實際數據的快速訪問,因為存儲在磁片上的大型資料庫中存儲的值的訪問是非常耗時的過程。
在最壞的情況下,搜索包含n個鍵值的未索引和未排序的資料庫需要O(n)運行時間。 但是,如果使用B樹來索引此資料庫,則在最壞的情況下將在O(log n)時間內搜索它。
