二叉樹是一種特殊類型的通用樹,它的每個節點最多可以有兩個子節點。 二叉樹通常被劃分為三個不相交的子集。
- 節點的根
- 左二叉樹。
- 右二叉樹
二叉樹的結構,如在下圖中顯示。
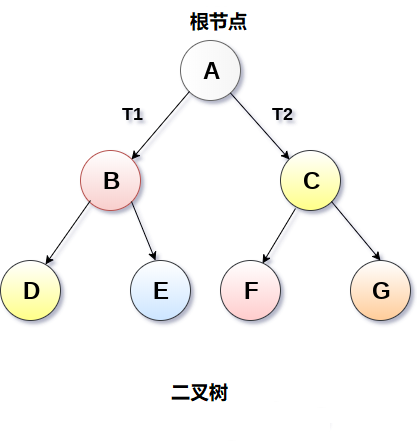
1. 二叉樹的類型
1.1. 嚴格二叉樹
在嚴格二叉樹中,每個非葉節點包含非空的左和右子樹。 換句話說,每個非葉節點的等級將始終為2。具有n個葉子的嚴格二叉樹將具有(2n-1)個節點。
嚴格二叉樹如下圖所示。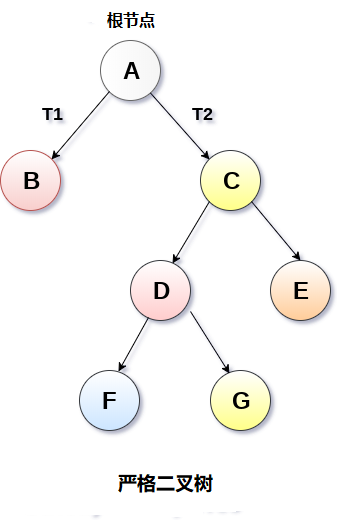
1.2. 完全二叉樹
如果所有葉子都位於相同的水準d,則稱二元樹是完全二叉樹。完全二叉樹是二叉樹,在0級和d級之間的每個級別包含正好2 ^ 1個節點。 具有深度d的完全二叉樹中的節點總數是2^d+1 -1,其中葉節點是2d而非葉節點是2^d-1。
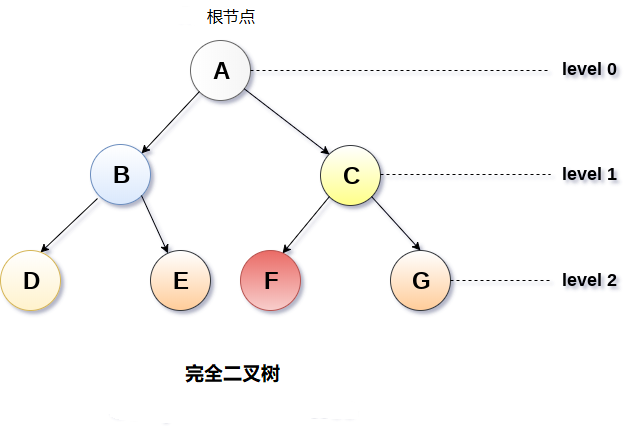
2. 二叉樹遍曆
二叉樹遍曆的方法有以下幾種:
| 編號 | 遍曆 | 描述 |
|---|---|---|
| 1 | 前序遍曆 | 首先遍曆根,然後分別遍曆左子樹和右子樹。 該過程將遞歸地應用於樹的每個子樹。 |
| 2 | 中序遍曆 | 首先遍曆左子樹,然後分別遍曆根和右子樹。 該過程將遞歸地應用於樹的每個子樹。 |
| 3 | 後序遍曆 | 遍曆左子樹,然後分別遍曆右子樹和根。 該過程將遞歸地應用於樹的每個子樹。 |
3. 二叉樹表示
二叉樹有兩種表示形式:
3.1. 鏈接表示
在這種表示中,二叉樹以鏈表的形式存儲在記憶體中,其節點的數量存儲在非連續的記憶體位置並通過像樹一樣繼承父子關係而鏈接在一起。 每個節點包含三個部分:指向左節點的指針,數據元素和指向右節點的指針。 每個二叉樹都有一個根指針,指向二叉樹的根節點。 在空二進位樹中,根指針將指向null。
如下圖中給出的二叉樹。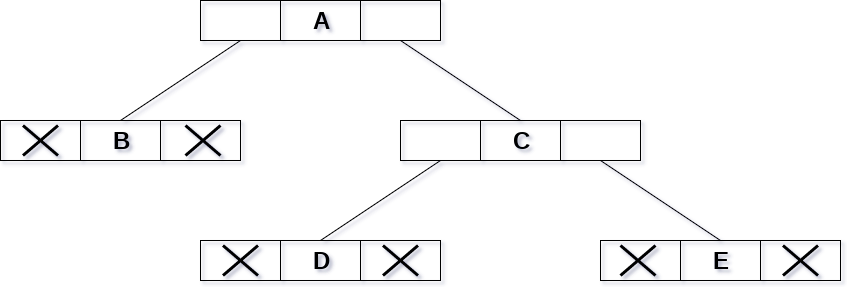
在上圖中,樹被視為節點的集合,其中每個節點包含三個部分:左指針,數據元素和右指針。 左指針存儲左子節點的地址,而右指針存儲右子節點的地址。 葉節點的左右指針包含null。
下圖顯示了如何使用鏈接表示為二叉樹分配記憶體。 記憶體中維護了一個特殊指針,指向樹的根節點。 樹中的每個節點都包含其左右子節點的地址。 葉節點的左右指針包含null。
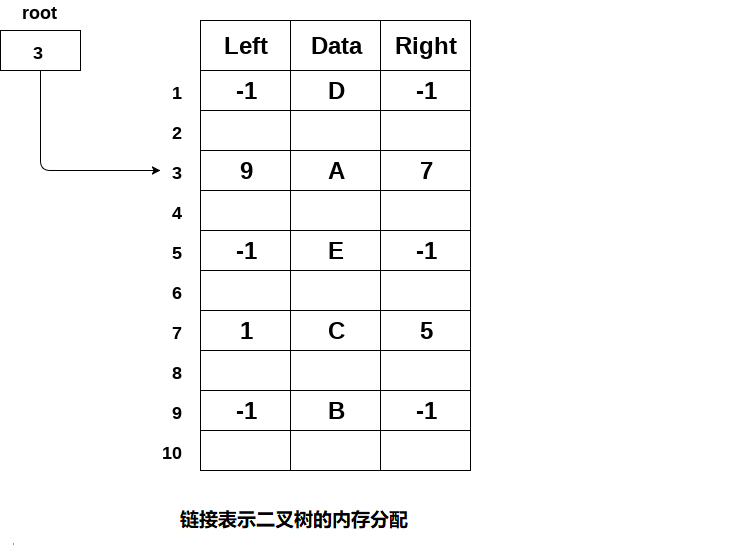
3.2. 順序表示
這是存儲樹元素的最簡單的記憶體分配技術,但它是一種效率低下的技術,因為它需要大量空間來存儲樹元素。 下圖顯示了二叉樹及其記憶體分配。
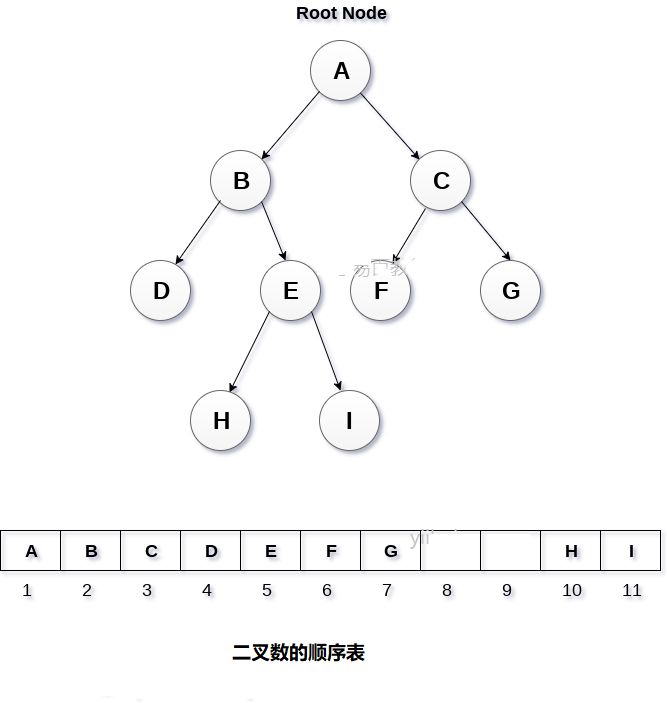
在這種表示方式中,數組用於存儲樹元素。 數組的大小將等於樹中存在的節點數。 樹的根節點將出現在數組的第一個索引處。 如果節點存儲在第i個索引處,則其左右子節點將存儲在2i和2i + 1位置。 如果數組的第一個索引,即tree[1]為0,則表示樹為空。
