深度優先搜索（DFS）演算法

深度優先搜索(DFS)演算法從圖G的初始節點開始，然後越來越深，直到找到目標節點或沒有子節點的節點。該演算法然後從死角回溯到尚未完全未探索的最新節點。

在DFS中使用的數據結構是堆疊。該過程類似於BFS演算法。 在DFS中，通向未訪問節點的邊稱為發現邊，而通向已訪問節點的邊稱為塊邊。

演算法

第1步：為G中的每個節點設置STATUS = 1(就緒狀態)
第2步：將起始節點A推入堆疊並設置其STATUS = 2(等待狀態)
第3步：重複第4步和第5步，直到STACK為空
第4步：彈出頂部節點N.處理它並設置其STATUS = 3(處理狀態)
第5步：將處於就緒狀態(其STATUS = 1)的N的所有鄰居推入堆疊並設置它們

    STATUS = 2(等待狀態)
    [迴圈結束]
第6步：退出

示例：

考慮圖G及其鄰接列表，如下圖所示。 通過使用深度優先搜索(DFS)演算法計算從節點H開始列印圖的所有節點的順序。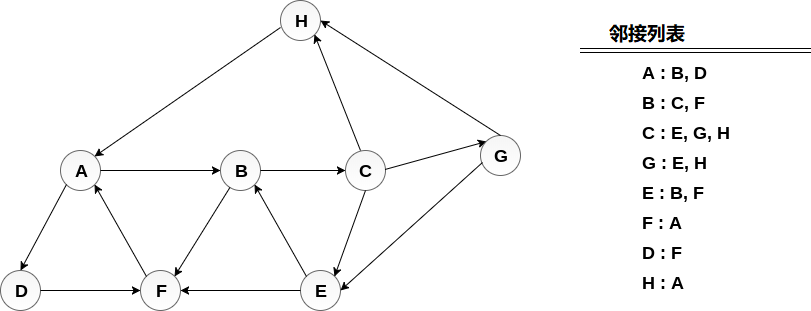

方案：
將H 推入堆疊 -

STACK : H

彈出是堆疊的頂部元素，即H，列印它並將H的所有鄰居推送到處於就緒狀態的堆疊上。

Print H
STACK : A

彈出堆疊的頂部元素，即A，列印它並將A的所有鄰居推入堆疊中處於就緒狀態。

Print A
Stack : B, D

彈出堆疊的頂部元素，即D，列印它並將D的所有鄰居推入處於就緒狀態的堆疊。

Print D
Stack : B, F

彈出堆疊的頂部元素，即F，列印它並將F的所有鄰居推入處於就緒狀態的堆疊。

Print F
Stack : B

彈出堆疊的頂部，即B並推送所有鄰居。

Print B
Stack : C

彈出堆疊的頂部，即C並推送所有鄰居。

Print C
Stack : E, G

彈出堆疊的頂部，即G並推送其所有鄰居。

Print G
Stack : E

彈出堆疊的頂部，即E並推送其所有鄰居。

Print E
Stack :

因此，堆疊現在變為空，並且遍曆了圖的所有節點。

圖表的列印順序為：

H → A → D → F → B → C → G → E