數據結構簡介

數據結構可以定義為數據元素組，它提供了在電腦中存儲和組織數據的有效方法，以便可以有效地使用它。 數據結構的一些示例是：數組，鏈表，堆疊，佇列等。數據結構廣泛用於電腦科學的幾乎每個方面，即操作系統，編譯器設計，人工智慧，圖形等等。

數據結構是許多電腦科學演算法的主要部分，因為它們使程式員能夠以有效的方式處理數據。 它在提高軟體或程式的性能方面發揮著重要作用，因為軟體的主要功能是盡可能快地存儲和檢索用戶的數據。

基本術語

數據結構是任何程式或軟體的構建塊(基礎塊)。為程式選擇適當的數據結構對於程式員來說是最困難的任務。就數據結構而言，使用以下術語 -

數據：數據可以定義為基本值或值集合，例如，學生的姓名和ID，成績等就是學生的數據。

組項：具有從屬資料項目的資料項目稱為組項，例如，學生的姓名由名字和姓氏組成。

記錄：記錄可以定義為各種資料項目的集合，例如，如果以學生實體為例，那麼學生的名稱，地址，課程和標記可以組合在一起形成學生的記錄。

檔：檔是一種類型實體的各種記錄的集合，例如，如果類中有60名員工，則相關檔中將有20條記錄，其中每條記錄包含有關每個員工的數據。

屬性和實體：實體表示某些對象的類。它包含各種屬性。每個屬性表示該實體的特定屬性。

字段：字段是表示實體屬性的單個基本資訊單元。

為什麼需要數據結構

隨著應用程式變得越來越複雜，數據量日益增加，可能會出現以下問題：

• 處理器速度：要處理非常大的數據，需要高速處理，但隨著數據逐日增長到每個實體數十億個檔，處理器可能無法處理大量數據。

• 數據搜索：假設商店的庫存大小是100860個商品，如果應用程式需要搜索某一特定商品，則每次需要遍曆100860個商品，這會導致搜索過程變慢。

• 大量請求：如果成千上萬的用戶在Web伺服器上同時搜索數據，在此過程中可能在短時會有一個非常大請求而導致伺服器處理不了。

為了解決上述問題，使用數據結構。組織數據以形成數據結構，使得不需要搜索所有專案並且可以立即搜索所需數據。

數據結構的優點

• 效率：程式的效率取決於數據結構的選擇。 例如：假設有一些數據，需要執行搜索特定記錄。 在這種情況下，如果在數組中組織數據，則需要逐個元素地搜索。 因此，在這裏使用數組可能效率不高。 有更好的數據結構可以使搜索過程像有序數組，二進位搜索樹或哈希表一樣高效。
• 可重用性：數據結構是可重用的，即當實現了特定的數據結構，就可以在其他地方使用它。也將數據結構的實現編譯到不同客戶端使用的程式庫中。
• 抽象：數據結構由ADT指定，它提供抽象級別。 客戶端程式僅通過介面使用數據結構，而不涉及實現細節。

數據結構分類

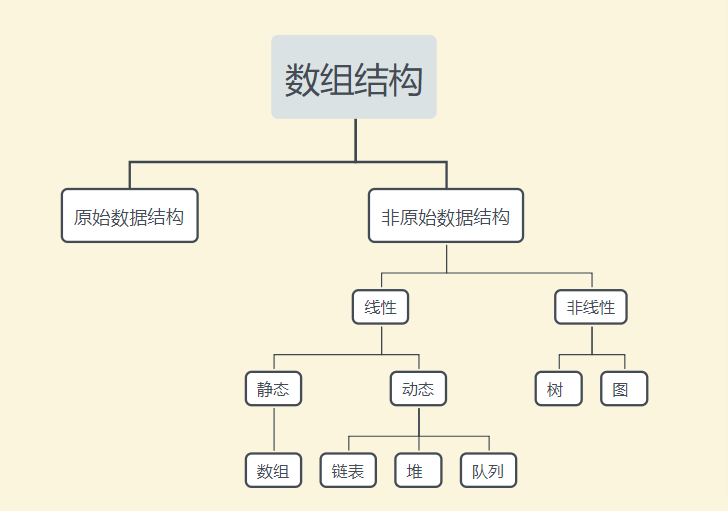
1. 線性數據結構

如果數據結構的所有元素按線性順序排列，則稱為線性數據結構。 線上性數據結構中，元素以非分層方式存儲，除了第一個和最後一個元素，它的每個元素具有後繼元素和前導元素。

線性數據結構的類型如下：

• 數組：數組是類似資料項目的集合，每個資料項目稱為數組的元素。 元素的數據類型可以是任何有效的數據類型，如char，int，float或double。
  數組的元素共用相同的變數名，但每個元素都帶有一個不同的索引號，這些索引號也稱為下標。 數組可以是一維的，二維的或多維的。

示例：數組age的各個元素是：

age[0], age[1], age[2], age[3],.... age[98], age[99]

• 鏈表：鏈表是一種線性數據結構，用於維護記憶體中的列表。 它可以看作存儲在非連續記憶體位置的節點集合。鏈表中的每個節點都包含指向其相鄰節點的指針。

• 堆疊 ：堆疊是一個線性列表，其中只允許在一端插入和刪除，稱為頂部。
  堆疊是一種抽象數據類型(ADT)，可以在大多數編程語言中實現。 它被命名為堆疊，因為它的行為類似於真實世界的堆疊，例如：成堆的板塊或卡片組等，只能在最頂面上操作。

• 佇列：佇列是一個線性列表，它的元素只能在一端插入(添加)，也被稱為後端，而只在另一端出隊(刪除)，也被稱為前端。

2. 非線性數據結構

非線性數據結構不形成序列，即每個專案或元素以非線性排列與兩個或更多個其他專案連接。 數據元素不按順序結構排列。

非線性數據結構的類型如下：

• 樹：樹是多級數據結構，其元素之間具有層次關係，樹的元素也稱為節點。層次中最底層的節點稱為葉節點，而最頂層節點稱為根節點。 每個節點都包含指向相鄰節點的指針。
  樹數據結構基於節點之間的父子關係。 除了葉節點之外，樹中的每個節點可以具有多個子節點，而除了根節點之外，每個節點可以具有最多一個父節點。 樹可以分為許多類別，本教程在稍後章節中將對此進行討論。

• 圖：圖可以定義為由稱為邊緣的鏈接連接的元素集(由頂點表示)的圖表示。 圖不同於樹，圖可以有迴圈而樹不能具有迴圈。

數據結構的操作

• 遍曆：每個數據結構都包含一組數據元素。遍歷數據結構表示訪問數據結構的每個元素，以便執行某些特定操作，如搜索或排序。示例 ：如果需要計算學生在6個不同科目中獲得的分數的平均值，需要遍曆完整的分數數組並計算總和，然後將總分數除以科目數，即6， 最後得到平均值。

• 插入：插入是在任何位置將元素添加到數據結構的過程。如果數據結構的大小是n，那麼只能在n-1個數據元素之間插入元素。

• 刪除：從數據結構中刪除元素的過程稱為刪除。 可以在任何隨機位置刪除數據結構中的元素。如果要從空數據結構中刪除元素，則會發生下溢。

• 搜索：在數據結構中查找元素位置的過程稱為搜索。 有兩種演算法可以執行搜索，即線性搜索和二進位搜索。在本教程後面討論這兩種搜索演算法。

• 排序：按特定順序排列數據結構的過程稱為排序。 有許多演算法可用於執行排序，例如，插入排序，選擇排序，冒泡排序等。

• 合併：當兩個列表分別為大小為M和N的列表A和列表B時，相似類型的元素，連接產生第三個列表，列表C的大小(M + N)，則此過程稱為合併。

以下是糾正/補充內容：