广度优先遍历

广度优先搜索算法

广度优先搜索算法(BFS)遍历图在广度运动并使用队列记得要获得下一个顶点，当穷途末路发生时迭代开始搜索。

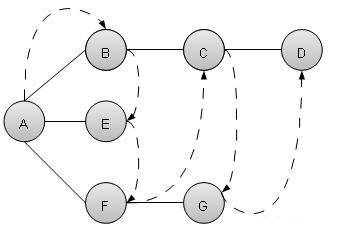
正如上面的例子给出的，BFS算法首先从A到B遍历到E到F，再到C和G最后到D. 它采用以下规则。

• 规则 1 − 访问邻近的未访问顶点。标记它访问并显示它。将其插入到队列中。

• 规则 2 − 如果没有相邻顶点发现，删除队列中的第一个顶点。

• 规则 3 − 重复第1条和第2条，直到队列为空。

void breadthFirstSearch(){
   int i;
	
   //mark first node as visited
   lstVertices[0]->visited = true;
	
   //display the vertex
   displayVertex(0);   
	
   //insert vertex index in queue
   insert(0);
	
   int unvisitedVertex;
   while(!isQueueEmpty()){
      //get the unvisited vertex of vertex which is at front of the queue
      int tempVertex = removeData();
		
      //no adjacent vertex found
      while((unvisitedVertex = getAdjUnvisitedVertex(tempVertex)) != -1){    
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         insert(unvisitedVertex);               
      }
   } 
	
   //queue is empty, search is complete, reset the visited flag        
   for(i = 0;i<vertexCount;i++){
      lstVertices[i]->visited = false;
   }    
}

演示程序

GraphDemo.c

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>

#define MAX 10

struct Vertex {
   char label;
   bool visited;
};

//stack variables

int stack[MAX]; 
int top = -1; 

//queue variables

int queue[MAX];
int rear = -1;
int front = 0;
int queueItemCount = 0;

//graph variables

//array of vertices
struct Vertex* lstVertices[MAX];

//adjacency matrix
int adjMatrix[MAX][MAX];

//vertex count
int vertexCount = 0;

//stack functions

void push(int item) { 
   stack[++top] = item; 
} 

int pop() { 
   return stack[top--]; 
} 

int peek() {         
   return stack[top];
}

bool isStackEmpty(){
   return top == -1;
}

//queue functions

void insert(int data){
   queue[++rear] = data;
   queueItemCount++;
}

int removeData(){
   queueItemCount--;
   return queue[front++]; 
}

bool isQueueEmpty(){
   return queueItemCount == 0;
}

//graph functions

//add vertex to the vertex list
void addVertex(char label){
   struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
   vertex->label = label;  
   vertex->visited = false;     
   lstVertices[vertexCount++] = vertex;
}

//add edge to edge array
void addEdge(int start,int end){
   adjMatrix[start][end] = 1;
   adjMatrix[end][start] = 1;
}

//display the vertex
void displayVertex(int vertexIndex){
   printf("%c ",lstVertices[vertexIndex]->label);
}       

//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex){
   int i;
	
   for(i = 0; i<vertexCount; i++)
      if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false)
         return i;
   return -1;
}

void depthFirstSearch(){
   int i;
	
   //mark first node as visited
   lstVertices[0]->visited = true;
	
   //display the vertex
   displayVertex(0);   
	
   //push vertex index in stack
   push(0);

   while(!isStackEmpty()){
      //get the unvisited vertex of vertex which is at top of the stack
      int unvisitedVertex = getAdjUnvisitedVertex(peek());
		
      //no adjacent vertex found
      if(unvisitedVertex == -1){
         pop();
      }else{
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         push(unvisitedVertex);
      }
   }

   //stack is empty, search is complete, reset the visited flag        
   for(i = 0;i < vertexCount;i++){
      lstVertices[i]->visited = false;
   }        
}

void breadthFirstSearch(){
   int i;
	
   //mark first node as visited
   lstVertices[0]->visited = true;
	
   //display the vertex
   displayVertex(0);   
	
   //insert vertex index in queue
   insert(0);
   int unvisitedVertex;
	
   while(!isQueueEmpty()){
      //get the unvisited vertex of vertex which is at front of the queue
      int tempVertex = removeData();   
      
      //no adjacent vertex found
      while((unvisitedVertex = getAdjUnvisitedVertex(tempVertex)) != -1){    
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         insert(unvisitedVertex);               
      }
   }   

   //queue is empty, search is complete, reset the visited flag        
   for(i = 0;i<vertexCount;i++){
      lstVertices[i]->visited = false;
   }    
}

main() {
   int i, j;

   for(i = 0; i<MAX; i++) // set adjacency
      for(j = 0; j<MAX; j++) // matrix to 0
         adjMatrix[i][j] = 0;

   addVertex('A');   //0
   addVertex('B');   //1
   addVertex('C');   //2
   addVertex('D');   //3
   addVertex('E');   //4
   addVertex('F');   //5
   addVertex('G');   //6

   /*      1  2  3   
   * 0  |--B--C--D
   * A--|
   * |
   * |     4 
   * |-----E
   * |     5  6
   * |  |--F--G
   * |--| 
   */        
   addEdge(0, 1);   //AB
   addEdge(1, 2);   //BC
   addEdge(2, 3);   //CD
   addEdge(0, 4);   //AC
   addEdge(0, 5);   //AF
   addEdge(5, 6);   //FG
	
   printf("Depth First Search: ");
   //A B C D E F G
   depthFirstSearch(); 
	
   printf("\nBreadth First Search: ");
   //A B E F C G D
   breadthFirstSearch();
}

如果我们编译并运行上述程序，那么这将产生以下结果 -

Depth First Search: A B C D E F G 
Breadth First Search: A B E F C G D