在二叉搜索树中删除元素

函数delete()用于从二叉搜索树中删除指定的节点。 但是，不能违反二叉搜索树的属性。 从二叉搜索树中删除节点有三种情况。

1. 要删除的节点是叶节点

这是最简单的情况，在这种情况下，用NULL替换叶节点并简单地释放分配的空间。
在下图中，假设要删除节点85，因为此节点是叶节点，因此节点将被替换为NULL并且将释放分配的空间。

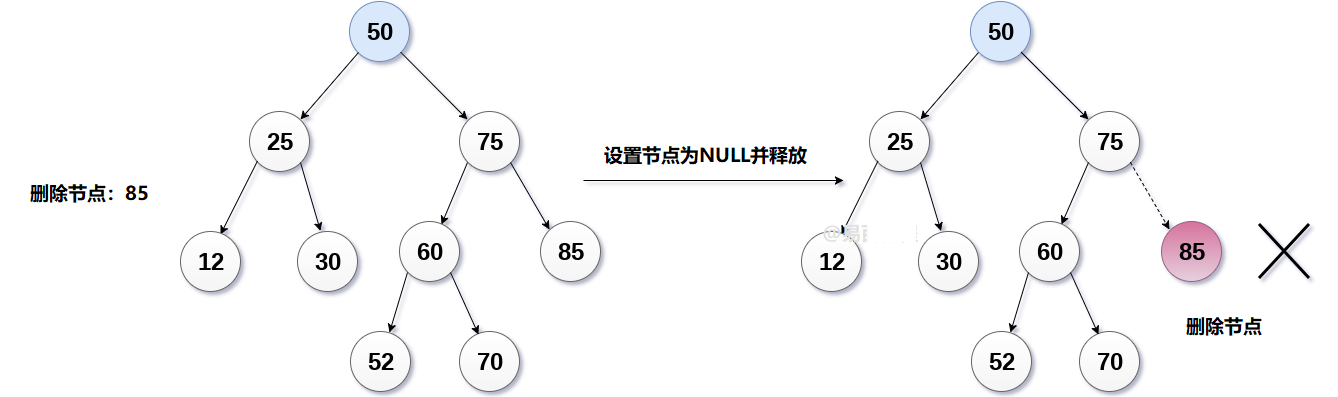
2. 要删除的节点只有一个子节点

在这种情况下，将节点替换为其子节点并删除子节点，该子节点现在包含要删除的值。 只需将其替换为NULL并释放分配的空间即可。

在下图中，将删除节点12。 它只有一个子节点。 该节点将被其子节点替换，并且将简单地删除替换的节点12(现在是叶节点)。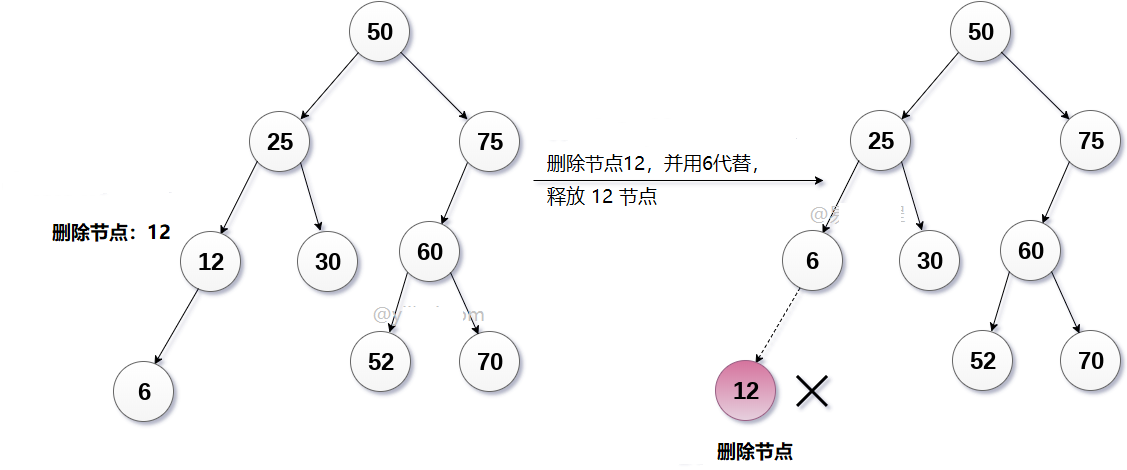

3. 要删除的节点有两个子节点

与上面的两种情况相比，这种情况有点复杂。 但是，要删除的节点被递归地替换为其有序后继或前导，直到将节点值(要删除)放置在树的叶子上。 在该过程之后，用NULL替换节点并释放分配的空间。

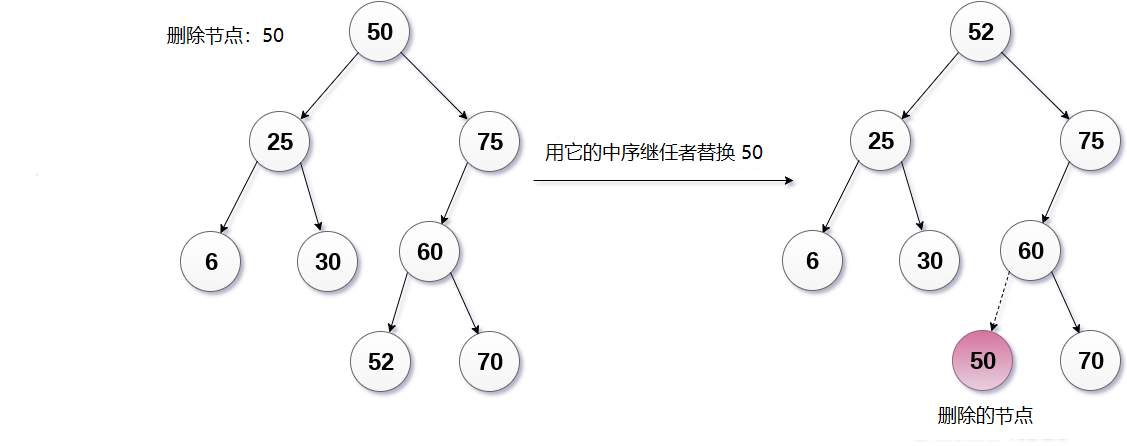
在下面的图像中，要删除节点50，它是树的根节点。 下面给出的树的有序遍历。

6, 25, 30, 50, 52, 60, 70, 75

用它的中序继任者替换50。现在，50将被移动到树的叶子，之后将被删除。

算法

Delete (TREE, ITEM)

第1步 : IF TREE = NULL
      提示： "item not found in the tree" ELSE IF ITEM < TREE -> DATA
     Delete(TREE->LEFT, ITEM)
     ELSE IF ITEM > TREE -> DATA
   Delete(TREE -> RIGHT, ITEM)
     ELSE IF TREE -> LEFT AND TREE -> RIGHT
     SET TEMP = findLargestNode(TREE -> LEFT)
     SET TREE -> DATA = TEMP -> DATA
      Delete(TREE -> LEFT, TEMP -> DATA)
     ELSE
   SET TEMP = TREE
   IF TREE -> LEFT = NULL AND TREE -> RIGHT = NULL
      SET TREE = NULL
     ELSE IF TREE -> LEFT != NULL
     SET TREE = TREE -> LEFT
     ELSE
    SET TREE = TREE -> RIGHT
     [IF结束]
  FREE TEMP
[IF结束]
第2步: 结束

使用C语言实现删除二叉搜索树的节点，如下 -

void deletion(Node*& root, int item)  
{  
    Node* parent = NULL;  
    Node* cur = root;  

    search(cur, item, parent);  
    if (cur == NULL)  
        return;  

    if (cur->left == NULL && cur->right == NULL)  
    {  
        if (cur != root)  
        {  
            if (parent->left == cur)  
                parent->left = NULL;  
            else  
                parent->right = NULL;  
        }  
        else  
            root = NULL;  

        free(cur);       
    }  
    else if (cur->left && cur->right)  
    {  
        Node* succ  = findMinimum(cur- >right);  

        int val = succ->data;  

        deletion(root, succ->data);  

        cur->data = val;  
    }  

    else  
    {  
        Node* child = (cur->left)? Cur- >left: cur->right;  

        if (cur != root)  
        {  
            if (cur == parent->left)  
                parent->left = child;  
            else  
                parent->right = child;  
        }  

        else  
            root = child;  
        free(cur);  
    }  
}  

Node* findMinimum(Node* cur)  
{  
    while(cur->left != NULL) {  
        cur = cur->left;  
    }  
    return cur;  
}