从AVL树中删除节点类似于二叉搜索树中删除节点。 删除可能会干扰AVL树的平衡因子,因此需要重新平衡树以保持AVL树平衡。 因此需要进行旋转。 两种类型的旋转是L旋转和R旋转。 在这里将讨论R旋转。L旋转是它们的镜像。
如果要删除的节点存在于关键节点的左子树中,则需要应用L旋转,否则,如果要删除的节点存在于关键节点的右子树中 ,将执行R旋转。
考虑一下,A是关键节点,B是其左子树的根节点。 如果要删除存在于A的右子树中的节点X,则可能存在三种不同的情况:
1. R0旋转(节点B的平衡系数为0)
如果节点B具有0平衡因子,并且在删除节点X时节点A的平衡因子受到干扰,则将通过使用R0旋转旋转树来重新平衡树。
关键节点A向右移动,节点B成为树的根,T1为左子树。 子树T2和T3成为节点A的左右子树,R0旋转中涉及的过程如下图所示。
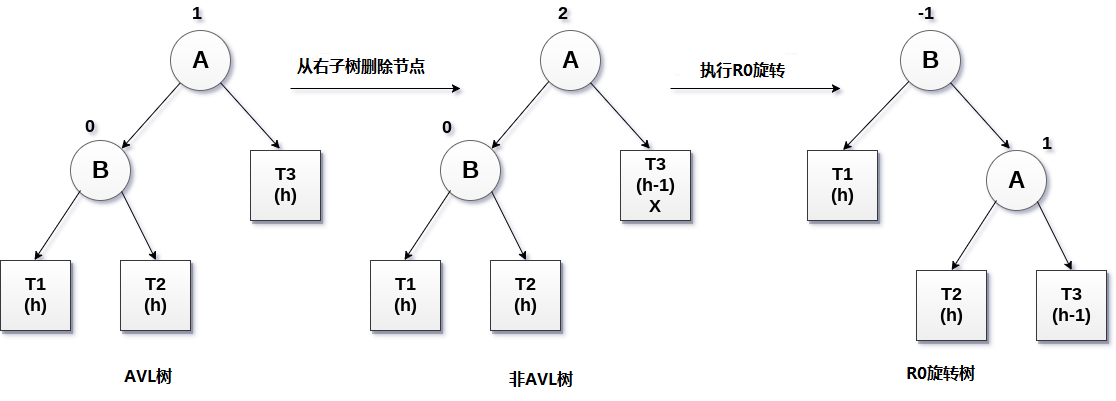
示例:
从下图中显示的AVL树中删除节点30。
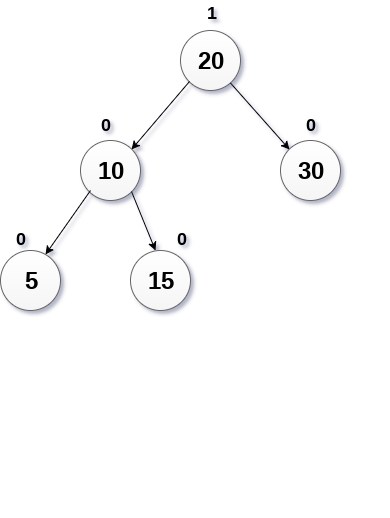
解释
在这种情况下,节点B具有平衡因子0,因此将通过使用R0旋转来旋转树,如下图所示。 节点B(10)成为根,而节点A向右移动。 节点B的右子节点现在将成为节点A的左子节点。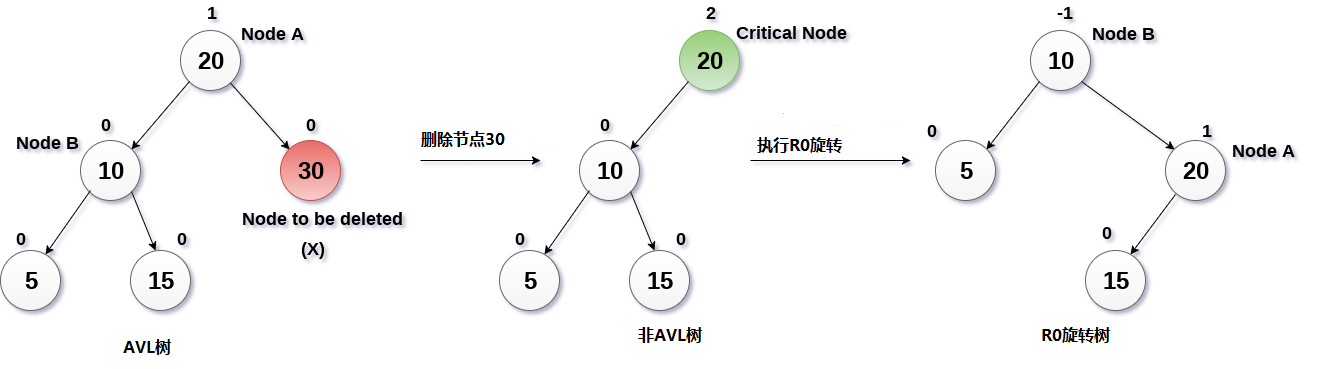
2. R1旋转(节点B具有平衡因子1)
如果节点B的平衡因子是1,则执行R1旋转。在R1旋转中,关键节点A向右移动,子树T2和T3分别作为其左和右子节点。 T1将被放置为节点B的左子树。
R1旋转涉及的过程如下图所示。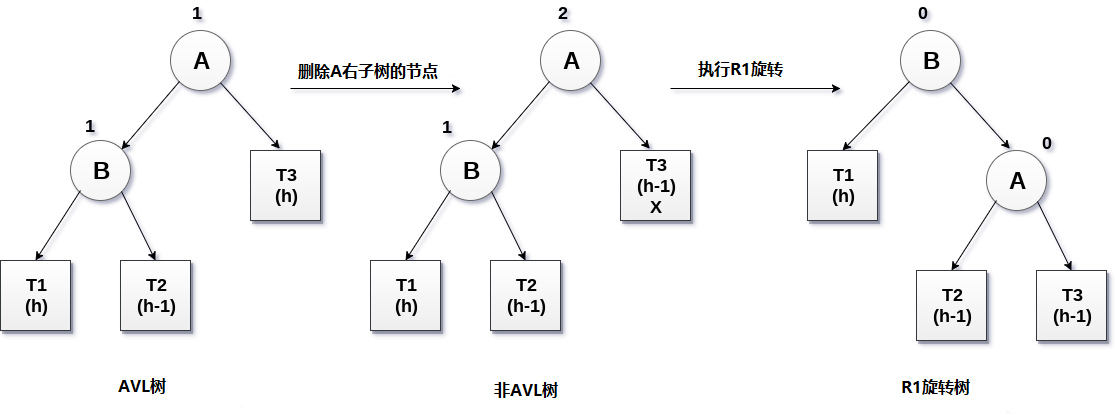
示例
从下图中显示将要删除AVL树中的节点55。
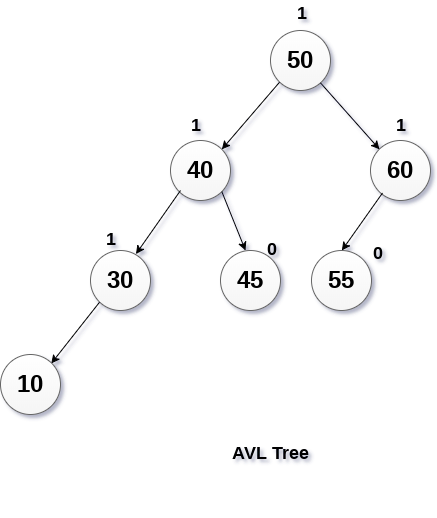
方案:
从AVL树中删除55节点,扰乱了节点50的平衡因子,即成为关键节点的节点A. 这是R1旋转的条件,其中节点A将向右移动(如下图所示)。 B的右侧现在变为A的左边(即45)。
解决方案中涉及的过程如下图所示。
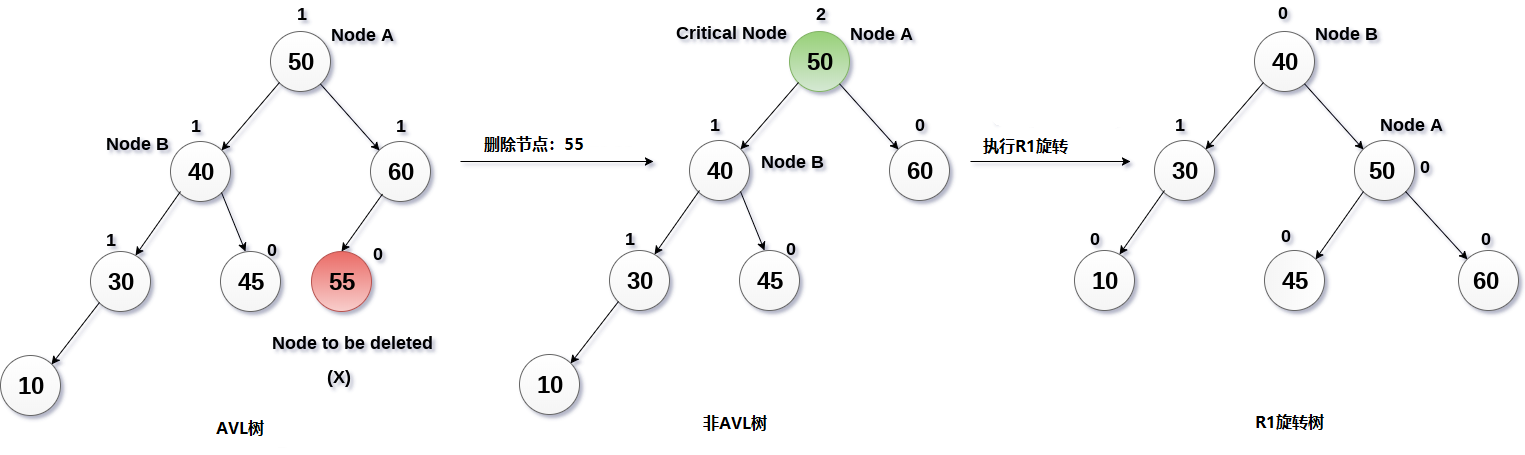
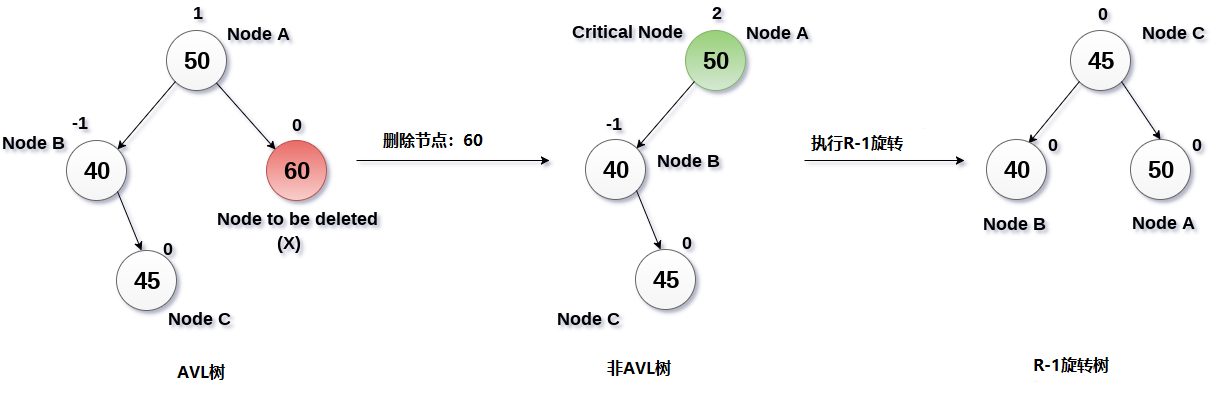
3. R-1旋转(节点B具有平衡因子-1)
如果节点B具有平衡因子-1,则执行R-1旋转。 这种情况的处理方式与LR旋转相同。 在这种情况下,作为节点B的右子节点的节点C成为树的根节点,其中B和A分别作为其左和右子节点。
子树T1,T2成为B的左右子树,而T3,T4成为A的左右子树。
R-1旋转涉及的过程如下图所示。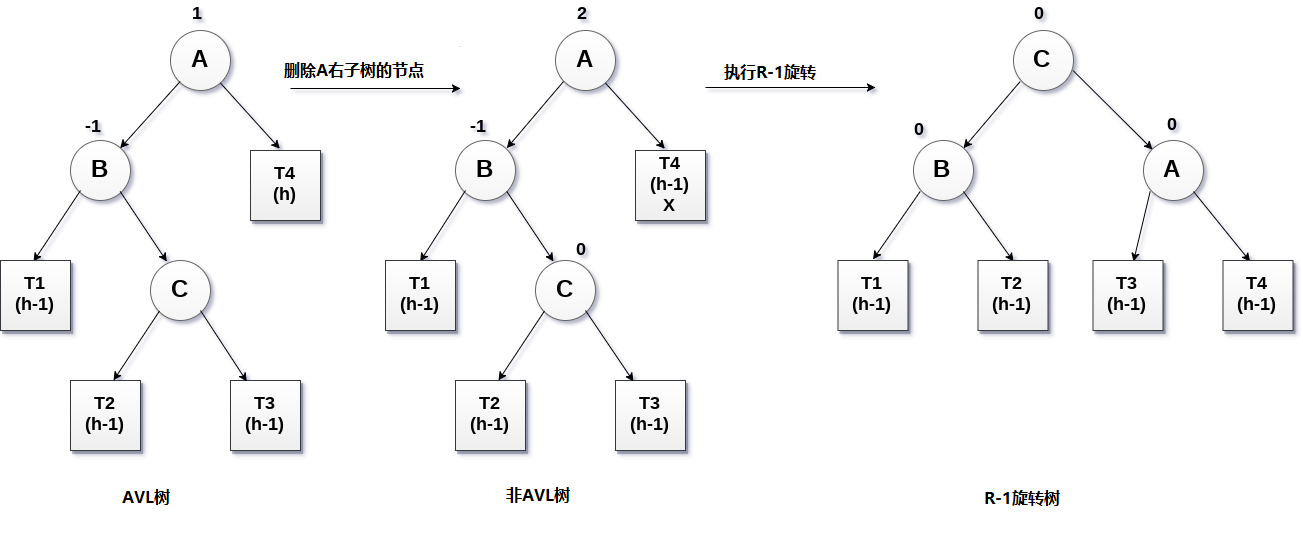
示例
从下图所示的AVL树中删除节点60。
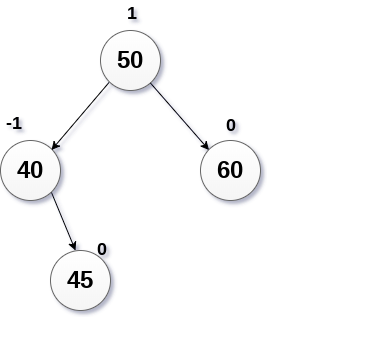
解答:
在这种情况下,节点B具有平衡因子-1。 因此,删除节点60会扰乱节点50的平衡因子,需要执行R-1旋转。 节点C即45成为树的根,节点B(40)和A(50)作为其左右子节点。